1 + T_k(k) x H(k; k) = T_k(k).

Если вычисления Т_k(k ) останавливаются, то мы приходим к противоречию (в этом случае Н(k; k) должно равняться единице, но тогда возникнет невыполнимое равенство: 1+Т_k(k ) = Т_k(k )). Значит, Т_k(k ) не может остановиться, т. е.

Т_k(k ) = ^□.

Но алгоритм не может этого «знать», потому что, если бы он давал Н(k; k) = 0, мы снова пришли бы к противоречию (мы получили бы тогда неверное соотношение 1+0=^□).

Таким образом, если мы можем отыскать k, то мы знаем, как построить вычислительную процедуру, для которой алгоритм не дает решения проблемы остановки, но нам ответ известен! А как нам найти k ? Это непростая задача. Необходимо тщательно изучить конструкцию H(n; m ) и T_n(m) и понять, как в точности действует 1 + Т_n(n ) х Н(n; n) в качестве машины Тьюринга. Затем надо определить номер этой машины, который и есть k. Конечно, это выполнить трудно, но вполне возможно [54] . Из-за этих трудностей вычисление Т_k(k ) нас бы вовсе не интересовало, не будь она специально предназначена для доказательства неэффективности алгоритма H! Важно то, что мы получили строго определенную процедуру, которая для любого наперед заданного алгоритма H позволяет найти такое k, что для Т_k(k ) этот алгоритм не может решить проблему остановки, т. е. мы тем самым превзошли его. Возможно, мысль о том, что мы «умнее» каких-то алгоритмов, принесет нам некоторое удовлетворение!

На самом деле, упомянутая процедура настолько хорошо определена, что мы могли бы даже найти алгоритм для нахождения k по заданному H. Поэтому, прежде чем мы «погрязнем» в самодовольстве, мы должны осознать, что этот алгоритм может улучшить H [55] , поскольку он, по сути, «знает», что Т_k(k) = ^□, - или все-таки нет? В предыдущем изложении было удобно использовать антропоморфный термин «знать» по отношению к алгоритму. Однако не мы ли в конечном счете «знаем», тогда как алгоритм просто следует определенным нами правилам? А может быть мы сами просто следуем правилам, запрограммированным в конструкции нашего мозга и в окружающей нас среде? Эта проблема затрагивает не только алгоритмы, но и то, как мы выносим суждения об истинности и ложности. К этим важнейшим проблемам мы вернемся позднее. Вопрос о математической истине (и ее неалгоритмической природе) будет рассмотрен в главе 4. На данный момент мы, по крайней мере, получили некоторое представление о значении слов «алгоритм» и «вычислимость» и достигли понимания некоторых из относящихся к ним вопросов.

Лямбда-исчисление Черча

Понятие вычислимости — очень важная и красивая математическая идея. Примечателен также и ее малый возраст в сравнении с другими столь же фундаментальными математическим проблемами: она была впервые выдвинута только в 1930-х годах. Эта проблема имеет отношение ко всем областям математики (хотя, справедливости ради, отметим, что большинство математиков пока не часто обращаются к вопросам вычислимости). Сила этой идеи связана отчасти с существованием четко определенных и все же неразрешимых математических операций (как, например, проблема остановки машины Тьюринга и некоторые другие, которые мы рассмотрим в главе 4). Если бы не было таких невычислимых объектов, то теория алгоритмической разрешимости не представляла бы особого интереса для математики. В конце концов, математики любят головоломки.

Задача о разрешимости определенной математической операции может их заинтриговать, особенно потому, что общее решение этой головоломки само по себе алгоритмически не разрешимо.

Следует сделать еще одно замечание. Вычислимость — это по-настоящему «абсолютная» математическая идея. Это абстрактное понятие, которое никак не зависит от какой-либо конкретной реализации в терминах «машин Тьюринга» в том виде, как я их описал выше. Как я уже указывал, нет необходимости придавать какое-либо специальное значение «лентам», «внутренним состояниям» и т. п., характерным для гениального, но тем не менее частного подхода Тьюринга. Существуют также и другие способы выражения идеи вычислимости, причем исторически первым было «лямбда-исчисление», предложенное американским логиком Алонзо Черчем совместно со Стивеном Клини. Процедура, предложенная Черчем, значительно отличалась от метода Тьюринга и была гораздо более абстрактна. Фактически, форма, в которой Черч изложил свою теорию, делала связь между ними и чем бы то ни было «механическим» совсем не очевидной. Главная идея, лежащая в основе процедуры Черча, абстрактна по своей сути — это математическая операция, которую сам Черч назвал «абстрагированием».

Мне кажется, что стоит привести краткое описание схемы Черча не только потому, что она подчеркивает математическую природу идеи вычислимости, не зависящую от конкретного понятия вычислительной машины, но и потому, что она иллюстрирует мощь абстрактных идей в математике. Читатель, не достаточно свободный в математике и не увлеченный излагаемыми математическими идеями как таковыми, скорее всего предпочтет сейчас перейти к следующей главе — и не утратит при этом нить рассуждений. Тем не менее я полагаю, что таким читателям будет небесполезно следовать за мной еще какое-то время и оценить чудесную по своей стройности и продуманности схему Черча (см. Черч [1941]).

В рамках этой схемы рассматривается «универсальное множество» различных объектов, обозначаемых, скажем, символами

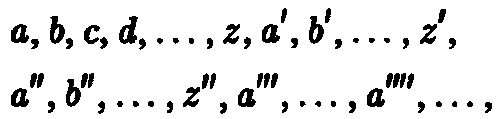
каждый из которых представляет собой математическую операцию, или функцию. (Штрихованные буквы позволяют создавать неограниченные наборы символов для обозначения таких функций.) «Аргументы» этих функций, т. е. объекты, на которые эти функции действуют, в свою очередь являются объектами той же природы, т. е. функциями. Более того, результат действия одной функции на другую (ее «значение») также представляет собой функцию. (Поистине, в системе Черча наблюдается замечательная экономия понятий.) Поэтому, когда мы пишем [56]

а = bс,

мы подразумеваем, что функция b, действуя на функцию c, дает в результате другую функцию а. В рамках этой схемы нетрудно сформулировать понятие функции двух или более переменных. Если мы хотим представить f как функцию двух переменных, скажем р и q, то мы можем просто написать

(fp)q

(что есть результат действия функции fp на функцию q ). Для функции трех переменных можно использовать выражение

((fp)q)r

и так далее.

Теперь мы можем перейти к описанию важнейшей операции абстрагирования. Для нее мы будем использовать греческую букву λ (лямбда). Непосредственно за ней будет следовать символ одной из функций Черча, скажем х, который мы будем рассматривать как «фиктивную переменную». Каждое появление х в квадратных скобках, следующих сразу за этим выражением, обозначает теперь просто место, куда подставляется все, что идет за всем этим выражением. Таким образом, когда мы пишем