Закон сохранения энергии — очень важный физический принцип. Это — не независимое физическое требование, а следствие из законов движения Ньютона, до которых мы скоро дойдем. На протяжении столетий все более понятные формулировки закона сохранения энергии делались Декартом, Гюйгенсом, Лейбницем, Эйлером и Кельвином. Позднее в этой главе и в главе 7 мы еще вернемся к закону сохранения энергии. Оказывается, что в сочетании с галилеевским принципом относительности закон сохранения энергии приводит к другим законам сохранения, имеющим немалое значение: закону сохранения массы и закону сохранения количества движения (импульса). Количество движения частицы равно произведению ее массы и ее скорости. Знакомые примеры сохранения количества движения возникают при рассмотрении реактивного движения, когда увеличение направленного вперед количества движения ракеты в точности уравновешивается направленным назад количеством движения выхлопных газов (обладающих меньшей массой, но зато большей скоростью). Отдача ружья при выстреле — еще одно проявление закона сохранения количества движения. Еще одним следствием из законов движения Ньютона служит закон сохранения углового момента (момента количества движения), описывающий постоянство вращения системы вокруг собственной оси. Вращение Земли вокруг собственной оси, равно как и вращение теннисного мяча вокруг собственной оси, не затухают благодаря закону сохранения их угловых моментов. Каждая частица, образующая любое тело, вносит свой вклад в полный угловой момент тела, причем величина этого вклада равна произведению количества движения частицы на расстояние ее от оси вращения (длину перпендикуляра, опущенного из точки, где находится частица, на ось вращения). (Следовательно, угловую скорость свободно вращающегося объекта можно увеличить, сделав объект более компактным. Это приводит к поразительному, но хорошо знакомому действию, часто исполняемому спортсменами на льду и воздушными гимнастами на трапеции. Прижав к себе руки или поджав ноги, они резко увеличивают скорость вращения просто вследствие закона сохранения углового момента!) Как будет показано в дальнейшем, масса, энергия, количество движения (импульс) и угловой момент принадлежат к числу важных для нас понятий. Наконец, мне следовало бы напомнить читателю о пророческой догадке Галилея, понявшего, что в отсутствие атмосферного сопротивления все тела под действием силы тяжести падают с одной и той же скоростью. (Возможно, читатель вспомнит известную легенду о том, как Галилей сбрасывал с наклонной башни в Пизе по несколько предметов одновременно.) Три столетия спустя то же самое озарение привело Эйнштейна к обобщению принципа относительности на ускоренные системы отсчета и стало, как мы увидим в конце этой главы, краеугольным камнем его необычайной общерелятивистской теории относительности.
На мощном фундаменте, заложенном Галилеем, Ньютону удалось возвести величественнейший храм. Он сформулировал три закона, управляющие поведением материальных тел. Первый и второй законы Ньютона по существу совпадали с законами, открытыми Галилеем: если на тело не действует никакая сила, то тело продолжает равномерно двигаться по прямой; если на тело действует какая-нибудь сила, то произведение массы тела на ускорение (т. е. скорость изменения количества движения тела) равно этой силе. Заслуга собственно Ньютона состояла в осознании необходимости третьего закона движения: сила, с которой тело А действует на тело В, в точности равна по величине и противоположна по направлению силе, с которой тело В действует на тело А (иными словами, «для каждого действия всегда существует равное по величине противодействие»), Три закона движения Ньютона образуют основу основ. «Ньютоновская вселенная» состоит из частиц, движущихся в пространстве, где действуют законы евклидовой геометрии.
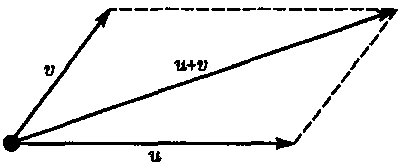
Рис. 5.6. Сложение векторов по правилу параллелограмма
Ускорения этих частиц определяются действующими на них силами. Сила, приложенная к каждой из частиц, получается путем сложения (по правилу сложения векторов, см. рис. 5.6) всех сил, действующих на данную частицу со стороны всех остальных частиц. Чтобы система была хорошо определенной, необходимо задать некоторое четкое правило, которое позволяло бы установить, какая сила действует на частицу А со стороны другой частицы В. Обычно мы требуем, чтобы эта сила действовала по прямой, соединяющей частицы А и В (рис. 5.7).

Рис. 5.7. Сила, действующая между двумя частицами, направлена по прямой между ними (и по третьему закону Ньютона сила, действующая на частицу А со стороны частицы В, всегда равна по величине и противоположна по направлению силе, действующей на В со стороны А)
Если речь идет о гравитационной силе, то между А и В возникает сила притяжения, величина которой пропорциональна произведению масс частиц А и В и обратно пропорциональна квадрату расстояния между частицами: закон обратных квадратов. Для других типов сил зависимость от взаимного расположения частиц может быть другой, и величина силы в этом случае будет зависеть не от масс частиц, а от какого-то иного их свойства.
Великий Иоганн Кеплер (1571–1630), современник Галилея, заметил, что орбиты планет, описываемые ими вокруг Солнца, имеют форму эллипсов, а не окружностей (причем Солнце всегда находится в фокусе, а не в центре эллипса), и сформулировал два других закона, задающих скорости, с которыми планеты движутся по орбитам. Ньютон сумел показать, что три закона Кеплера следуют из его собственной общей модели (с учетом силы притяжения, обратно пропорциональной квадрату расстояния между телами). Кроме того, Ньютон внес многие поправки к кеплеровским эллиптическим орбитам, а также объяснил ряд других эффектов (например, медленное движение оси вращения Земли, замеченное задолго до Ньютона еще древними греками). Чтобы прийти к таким результатам, Ньютону, помимо дифференциального исчисления, пришлось разработать немало дополнительных математических методов. Феноменальный успех, увенчавший эти усилия, во многом объясняется его высочайшим искусством математика и великолепной физической интуицией.
Механистический мир динамики Ньютона
С введением определенного закона для силы (как обратного квадрата расстояния между телами) ньютоновская модель превращается в точную и определенную систему динамических уравнений. Если положения, скорости и массы различных частиц заданы в некоторый момент времени, то их положения и скорости (равно как и массы, которые считаются постоянными) автоматически определены для всех последующих моментов времени. Эта форма детерминизма, которой удовлетворяет мир механики Ньютона, оказала (и все еще продолжает оказывать) глубокое влияние на философскую мысль. Попробуем изучить природу ньютонианского детерминизма чуть более подробно. Что он может сказать нам о «свободе воли»? Мог бы в строго ньютонианском мире существовать разум? Найдется ли в нем место хотя бы компьютерам?
Давайте попытаемся представить более конкретно «ньютонианскую» модель мира. Например, мы можем предположить, что частицы материи допустимо считать математическими точками, т. е. объектами, не имеющими никакой пространственной протяженности. В качестве альтернативы все частицы можно считать твердыми сферическими шариками. И в том, и в другом случае нам придется предположить, что законы действия сил, как в случае ньютоновского закона всемирного тяготения, известны. Мы хотим промоделировать и другие встречающиеся в природе силы, такие как электрические и магнитные взаимодействия (впервые подробно исследованные в 1600 году Уильямом Гильбертом), или сильные ядерные взаимодействия, которые, как ныне известно, связывают частицы (протоны и нейтроны), образующие атомные ядра. Электрическое взаимодействие похоже на гравитационное, поскольку тоже удовлетворяет закону обратных квадратов, но при этом одинаково заряженные частицы отталкивают (а не притягивают, как в случае гравитационного взаимодействия) друг друга, и величину электрического взаимодействия определяют не массы, а электрические заряды частиц. Магнитное взаимодействие, так же как и электрическое, «обратно пропорционально квадрату расстояния» [108] , но ядерное взаимодействие имеет совершенно другую зависимость от расстояния: оно очень велико на очень малых расстояниях, сравнимых с внутриатомными, и пренебрежимо мало на бо́льших расстояниях.
