Но в то же время можно сказать и обратное: что в некотором (практическом) смысле этот мир «невычислим», поскольку точность, с которой могут быть известны начальные данные, всегда ограничена. Действительно, такого рода задачам всегда присуща некоторая (и весьма значительная) «нестабильность». Очень небольшое изменение в начальных условиях может привести к возникновению чудовищных изменений в конечном состоянии. (Всякий, кто пытался загнать в лузу бильярдный шар, стремясь ударить его промежуточным шаром, поймет, что я имею в виду!) Сказанное становится очевидным, когда происходят (последовательные) столкновения, но такие неустойчивости в поведении могут встречаться и в случае действия ньютоновского тяготения на расстоянии (если гравитирующих тел больше двух). Для обозначения этого типа неустойчивости часто используется термин «хаос», или «хаотическое поведение». Например, хаотическое поведение важно, когда речь заходит о погоде. Хотя ньютоновские уравнения, управляющие стихиями, хорошо изучены, долговременный прогноз погоды печально известен своей ненадежностью!

Все это не похоже на тот тип «невычислимости», который можно было бы каким-то образом «использовать». Невычислимость в данном случае обусловлена просто тем, что из-за существования предела точности, с которой может быть известно начальное состояние, будущее состояние в принципе не поддается точному расчету на основании известных начальных условий. На самом деле, в этом случае к будущему поведению системы примешивается случайный элемент — и только. Если же работа мозга все-таки опирается на полезные невычислимые составляющие физических законов, то последние должны быть совершенно другими — и более конструктивными — по своей природе. Поэтому я не буду называть «хаотическое» поведение такого рода «невычислимостью», предпочитая использовать термин «непредсказуемость». Наличие непредсказуемости — весьма общее явление для тех детерминистских законов, которые, как мы вскоре убедимся, действительно возникают в (классической) физике. Но мы скорее уж предпочтем минимизировать непредсказуемость, чем «использовать» ее в конструкции мыслящей машины!

Обсуждая в общем и целом вопросы вычислимости и непредсказуемости, нам будет полезно принять более широкую, чем прежде, точку зрения на природу физических законов. Это позволит рассматривать не только схему ньютоновской механики, но и более поздние теории, пришедшие ей на смену. И сперва нам стоит окинуть беглым взглядом замечательную формулировку законов механики, предложенную Гамильтоном.

Гамильтонова механика

Своими успехами ньютоновская механика обязана не только своей способности исключительно точно описывать физический мир, но и обилию порожденных ею математических теорий. Замечательно, что все ПРЕВОСХОДНЫЕ теории природы оказались весьма щедрыми источниками математических идей. В этом кроется глубокая и прекрасная тайна: все наиболее точные теории в то же время необычайно плодотворны и с точки зрения математики. Не подлежит сомнению, что это свидетельствует о каких-то глубоких связях между реальным окружающим нас миром и платоновским миром математики. (Далее, (в главе 10, «Взгляд на физическую реальность») я постараюсь еще раз вернуться к этому вопросу.) Возможно, ньютоновская механика в этом отношении не имеет себе равных, так как ее рождение привело к возникновению дифференциального и интегрального исчисления. Кроме того, специфическая ньютонианская схема дала рождение массе замечательных математических идей, составляющих классическую механику. Имена многих великих математиков XVIII и XIX веков связаны с развитием этой науки: Эйлер, Лагранж, Лаплас, Лиувилль, Пуассон, Якоби, Остроградский, Гамильтон. То, что принято называть «гамильтоновой теорией» [112] включает в себя многое из проделанной ими работы. Сейчас мы вкратце коснемся Общих положений этой теории. Разносторонний и самобытный ирландский математик Уильям Роуан Гамильтон (1805–1865), автор гамильтоновых циклов (обсуждаемых в гл.4, подгл. «Теория сложности»), придал этой теории такую форму, которая особо подчеркивала аналогию с распространением волн. Это указание на существование взаимосвязи между волной и частицей (равно как и форма самих уравнений Гамильтона) сыграло важную роль в последующем развитии квантовой механики. К этой стороне дела я еще вернусь в следующей главе.

В рамках гамильтоновой теории впервые появились «переменные» для описания физической системы. До Гамильтона положения частиц считались первичными, а скорости считались просто быстротой изменения положения частиц во времени. Напомним, что для задания начального состояния ньютоновской системы нам необходимы положения и скорости всех частиц — только тогда мы можем определить последующее поведение системы. В рамках гамильтоновой формулировки необходимо выбирать импульсы, а не скорости частиц. (В гл.5, подгл. «Динамика Галилея и Ньютона» мы отметили, что импульс частицы есть не что иное, как произведение ее скорости на массу.) Само по себе это нововведение может показаться несущественным, но важно здесь другое: положение и импульс каждой частицы в гамильтоновой формулировке надлежит рассматривать как независимые, более или менее равноправные величины. Тем самым, используя гамильтонову формулировку, мы «делаем вид», что импульсы различных частиц не имеют никакого отношения к быстроте изменения переменных, описывающих их относительное положение, а представляют собой отдельный набор переменных — и, как следствие, мы можем считать импульсы совершенно независимыми от изменения положений движущихся частиц. В гамильтоновой формулировке мы располагаем двумя системами уравнений: одна из них говорит нам о том, как изменяются во времени импульсы различных частиц, другая — о том, как изменяются во времени положения частиц. И в том, и в другом случае быстрота изменений определяется различными положениями и импульсами в рассматриваемый момент времени.

Грубо говоря, первая система гамильтоновых уравнений выражает второй, самый важный закон движения Ньютона (быстрота изменения импульса = силе), тогда как вторая система уравнений Гамильтона говорит нам о том, чему равны импульсы, выраженные в терминах скоростей (быстрота изменения положения = импульс/массу). Напомним, что в формулировках законов движения Галилея — Ньютона использовались ускорения (или быстрота изменения быстроты изменения положения, т. е. уравнения «второго порядка»), тогда как в гамильтоновой формулировке нам достаточно говорить только о быстроте изменения величин (уравнения «первого порядка»). Все гамильтоновы уравнения выводятся всего лишь из одной важной величины: функции Гамильтона Н, представляющую собой полную энергию системы, выраженную в переменных, описывающих положения и импульсы.

Гамильтонова формулировка дает весьма изящное и симметричное описание механики. Выпишем здесь гамильтоновы уравнения просто для того, чтобы понять, как они выглядят, хотя многие читатели, возможно, и не знакомы с принятыми в математическом анализе обозначениями, необходимыми для полного понимания — впрочем, оно сейчас и не требуется. Все, что нам сейчас действительно нужно знать о дифференциальном исчислении, ограничивается пониманием смысла «точки» в левых частях уравнений Гамильтона — она означает быстроту изменения по времени (в первом случае — импульса, во втором случае — положения):

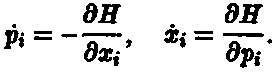
Индекс i здесь использован просто для того, чтобы отличать все различные координаты импульсов (р₁, p₂, p₃, p₄…) и положений (х₁, х₂, x₃, x₄…). Для n частиц, не ограниченных наложенными на них связями, мы получаем 3n координат импульсов и 3n координат положений (по одной координате для каждого из трех независимых направлений в пространстве). Символ ∂ относится к операции «частного дифференцирования» (взятию производной по одной переменной при сохранении постоянных значений всех остальных переменных), а Н, как сказано выше, означает функцию Гамильтона. (Если Вы ничего не знаете о «дифференцировании» — не стоит беспокоиться. Просто рассматривайте правые части уравнений Гамильтона как некие вполне определенные математические выражения, записанные через x_i и p_i.)